Question

The function h(t) = –16t(t – 2) + 24 models the height h, in feet, of a ball t seconds after it is thrown straight up into the air. What is the initial velocity and the initial height of the ball?

Answer 1

Initial velocity = 32 ft/s

Initial height = 24 ft.

Explanation

The function gives us the function that models the height, h, in feet for the ball as a function of time, t, in seconds.

h(t) = -16t (t - 2) + 24

We are then asked to find the initial velocity and the initial height of the ball.

This means we find the velocity and the height of the ball at t = 0

Velocity is given as the first derivative of the height function

v = (dh/dt)

h(t) = -16t (t - 2) + 24

h(t) = -16t² + 32t + 24

v = (dh/dt) = -32t + 32

When t = 0

v = -32t + 32 = -32 (0) + 32 = 0 + 32 = 32 ft/s

Initial velocity = 32 ft/s

For the initial height, t = 0

h(t) = -16t (t - 2) + 24

h(t) = -16t² + 32t + 24

h(0) = -16(0²) + 32(0) + 24

h(0) = 0 + 0 + 24

h(0) = 24 ft

Initial height = 24 ft.

Answer 2

The initial velocity of the ball is 32 feet per second.

The initial height of the ball is 24 feet.

Explanation:

Velocity is the rate of change of distance with respect to time.

Therefore, to find the equation for velocity, differentiate the height function with respect to time.

`\begin{aligned} h(t) &= -16t(t - 2) + 24\\&= -16t^2+32t+24\\\\\implies v=h'(t)&=-32t+32\end{aligned}`

The initial velocity of the ball is its velocity when t = 0.

Therefore, at time t = 0, the velocity is:

`\begin{aligned}\implies v=h'(0)&=-32(0)+32\\&=32\sf\;ft\;s^(-1)\end{aligned}`

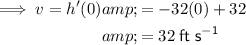
Therefore, the initial velocity of the ball is 32 feet per second.

The initial height of the ball is the height when t = 0.

Therefore, at time t = 0, the height of the ball is:

`\begin{aligned} \implies h(0) &= -16(0)(0 - 2) + 24\\&= 0+24\\&=24\sf\;ft\end{aligned}`

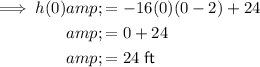
Therefore, the initial height of the ball is 24 feet.