Question

Find the equation of the straight line passing through the point (0,2) which is perpendicular to the line y=1/4x+5

Answer 1

y = -4x + 2

Explanation:

you need to find the gradient first and in order to find it, you need to look at the equation of the line given

in the equation, it refers to y = mx + c and from there, the gradient is whatever the value of m is. So in this situation, m = 1/4

now that you've found your gradient, you need to get the gradient when it is perpendicular (as stated in the question) by using m¹ x m² = -1

m¹ represents the gradient of the line we have whereas m² represents the gradient of the line we want so you just have to substitute 1/4 into m¹

`(1)/(4) * {m}^(2) = - 1`

`{m}^(2) = ( - 1)/(( (1)/(4) ))`

`{m}^(2) = - 4`

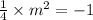
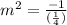
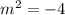
now you need to find the c of the y = mx + c before you complete the equation

y = 2 (from the question)

x = 0 (from the question)

m = -4

(2) = (-4)(0) + c

2 = c

c = 2

and you just substitute everything except y into y = mx + c and you're done

y = -4x + 2