Question

A line passes through points (3,20) and (8,25). Write a linear function rule in terms of x and y for this line.

Answer 1

To find:-

• The equation of line passing through the points (3,20) and (8,25) .

Answer:-

To find out the equation of the line , we need to find out the slope first. It can be calculated as ,

`\implies m =(\Delta y)/(\Delta x )=(y_2-y_1)/(x_2-x_1) \\`

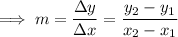
And here ,

• 
  `y_1` = 20
• 
  `y_2` = 25
• 
  `x_1` = 3
• 
  `x_2` = 8

On substituting the respective values, we have;

`\implies m =(25-20)/(8-3) \\`

`\implies m=(5)/(5)\\`

`\implies m=\boxed{1} \\`

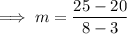
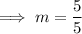
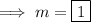
Hence the slope of the line is 1 . Now we may use point slope form of the line to find out the equation of the line. Point slope form of the line is,

`\implies y - y_1 = m(x-x_1) \\`

Take any of the given two points. Here i am taking (3,20) . So here we have;

• 
  `m` = 1
• 
  `y_1` = 20
• 
  `x_1` = 3

On substituting the respective values, we have;

`\implies y - 20 = 1(x - 3) \\`

`\implies y -20 = x - 3 \\`

`\implies x - 3 - y +20 = 0 \\`

`\implies \underline{\underline{\green{ x - y +17=0}}}\\`

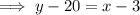
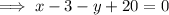
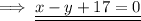
Hence the equation of the line in standard form is x - y + 17 = 0 .

and we are done!