Question

O is the centre of this circle.
What is the size of angle x?
Fully justify your answer.

Answer 1

In quadrilateral ABCD, given that
`\angle B=86^(\circ)`, and the center of the circle is O, the size of angle
`x` is 94°.

To determine the size of angle x in quadrilateral ABCD, we need to use the property that the sum of angles in a quadrilateral is 360 degrees.

Given:

`\begin{aligned}& \angle B=86^(\circ) \\& \angle D=x\end{aligned}`

In a quadrilateral, the sum of all angles is
`360^(\circ)`.Therefore,

`\angle A+\angle B+\angle C+\angle D=360^(\circ)`

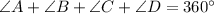
Substitute the given values:

`\angle A+86^(\circ)+\angle C+x=360^(\circ)`

Now, we know that opposite angles in a cyclic quadrilateral are supplementary. In other words, if a quadrilateral is inscribed in a circle, opposite angles are supplementary. Since
`\angle B` and
`\angle D` are opposite angles in the cyclic quadrilateral ABCD, we can say that:

`\angle B+\angle D=180^(\circ)`

Substitute the values:

`86^(\circ)+x=180^(\circ)`

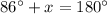
Now, solve for x:

`\begin{aligned}& x=180^(\circ)-86^(\circ) \\& x=94^(\circ)\end{aligned}`

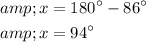
So, the size of angle
`x` is
`94^(\circ)`, and this is justified by using the properties of angles in a quadrilateral and the fact that opposite angles in a cyclic quadrilateral are supplementary.

Answer 2

x = 94°

Explanation:

ABCD is a cyclic quadrilateral , its 4 vertices lie on the circle.

the opposite angles of a cyclic quadrilateral sum to 180° , that is

x + 86° = 180° ( subtract 86° from both sides )

x = 94°