Question

Find the value of the derivative (if it exists) at
each indicated extremum

Answer 1

The value of the derivative at (2, 3) is zero.

Explanation:

Given function:

`g(x)=x+(4)/(x^2)`

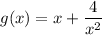
To differentiate the given function, use the power rule of differentiation.

`\boxed{\begin{minipage}{5.4 cm}\underline{Power Rule of Differentiation}\\\\If $y=x^n$, then $\frac{\text{d}y}{\text{d}x}=nx^(n-1)$\\\end{minipage}}`

`\textsf{Rewrite\;the\;function\;using\;the\;exponent\;rule\;\;$a^(-n)=(1)/(a^n)$}:`

`\implies g(x)=x+4x^(-2)`

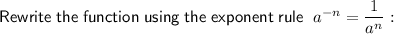
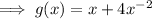
Apply the power rule:

`\implies g'(x)=1+(-2) \cdot 4x^(-2-1)`

`\implies g'(x)=1-8x^(-3)`

`\implies g'(x)=1-(8)/(x^3)`

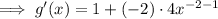
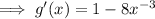
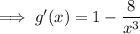
An extremum is a point where a function has a maximum or minimum value. From inspection of the given graph, the minimum point of the function is (2, 3).

To determine the value of the derivative at the minimum point, substitute x = 2 into the differentiated function.

`\begin{aligned}\implies g'(2)&=1-(8)/(2^3)\\\\&=1-(8)/(8)\\\\&=1-1\\\\&=0\end{aligned}`

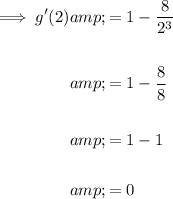
Therefore, the value of the derivative at (2, 3) is zero.