Question

Find the value of the derivative (if it exists) at
each indicated extremum

Answer 1

The value of the derivative at (-2/3, 2√3/3) is zero.

Explanation:

Given function:

`f(x)=-3x√(x+1)`

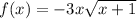
To differentiate the given function, use the product rule and the chain rule of differentiation.

`\boxed{\begin{minipage}{5.4 cm}\underline{Product Rule of Differentiation}\\\\If $y=uv$ then:\\\\$\frac{\text{d}y}{\text{d}x}=u\frac{\text{d}v}{\text{d}x}+v\frac{\text{d}u}{\text{d}x}$\\\end{minipage}}`


`\boxed{\begin{minipage}{7 cm}\underline{Differentiating $[f(x)]^n$}\\\\If $y=[f(x)]^n$, then $\frac{\text{d}y}{\text{d}x}=n[f(x)]^(n-1) f'(x)$\\\end{minipage}}`

`\begin{aligned}\textsf{Let}\;u &= -3x& \implies \frac{\text{d}u}{\text{d}{x}} &= -3\\\\\textsf{Let}\;v &= √(x+1)& \implies \frac{\text{d}v}{\text{d}{x}} &=(1)/(2) \cdot (x+1)^{-(1)/(2)}\cdot 1=(1)/(2√(x+1))\end{aligned}`

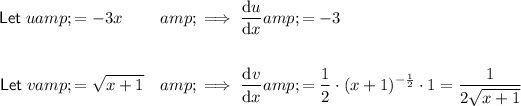
Apply the product rule:

`\implies f'(x) =u\frac{\text{d}v}{\text{d}x}+v\frac{\text{d}u}{\text{d}x}`

`\implies f'(x)=-3x \cdot (1)/(2√(x+1))+√(x+1)\cdot -3`

`\implies f'(x)=- (3x)/(2√(x+1))-3√(x+1)`

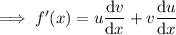
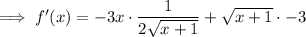
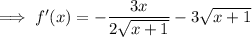
Simplify:

`\implies f'(x)=- (3x)/(2√(x+1))-(3√(x+1) \cdot 2√(x+1))/(2√(x+1))`

`\implies f'(x)=- (3x)/(2√(x+1))-(6(x+1))/(2√(x+1))`

`\implies f'(x)=- (3x+6(x+1))/(2√(x+1))`

`\implies f'(x)=- (9x+6)/(2√(x+1))`

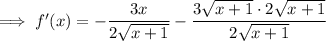
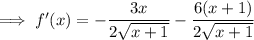
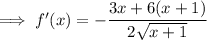
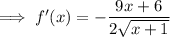
An extremum is a point where a function has a maximum or minimum value.

From inspection of the given graph, the maximum point of the function is (-2/3, 2√3/3).

To determine the value of the derivative at the maximum point, substitute x = -2/3 into the differentiated function.

`\begin{aligned}\implies f'\left(-(2)/(3)\right)&=- \frac{9\left(-(2)/(3)\right)+6}{2\sqrt{\left(-(2)/(3)\right)+1}}\\\\&=-\frac{0}{2\sqrt{(1)/(3)}}\\\\&=0 \end{aligned}`

Therefore, the value of the derivative at (-2/3, 2√3/3) is zero.