Question

The area of the intersection of a circle and a triangle is 45% of the area of their union. The area of the triangle outside the circle is 40% of the area of their union. What percentage of the circle lies outside the triangle?

Answer 1

Percentage of the circle that lies outside the triangle = 15%

Explanation:

Given,

The area of the intersection of circle and triangle is 45% of the area of the union.

The area of the triangle outside of the circle is 40% of the area of their union.

Required to find,

The percentage of the circle lies outside the triangle

Let us take 'C' as the area of the circle and 'T' as the area of the triangle.

The union of the area of the circle and triangle = C∪T

Let CUT be A

and the percentage of the circle that lies outside the triangle be 'x'

The intersection of the area of the circle and triangle = C∩T

Area of the triangle outside the circle = T - C

Area of the circle outside the triangle = C - T

Given,

C∩T = 45% of CUT = 45% of A

T - C = 40% of CUT = 40% of A

We know that,

The union of the area of the circle and triangle = Area of The intersection of the area of the circle and triangle + Area of the triangle outside the circle + Area of the circle outside the triangle

(CUT) = (C∩T) + (T - C) + (C - T)

`A = 45\%A + 40\%A + x\%A`

`A = (85+x)\% A`

`85 +x = 100`

∴
`x = 15`

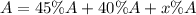
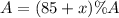
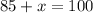
Percentage of the circle that lies outside the triangle = 15%