Question

Find the value of the derivative (if it exists) at
each indicated extremum.

Answer 1

The value of the derivative at (0, 0) is zero.

Explanation:

Given function:

`f(x)=(x^2)/(x^2+4)`

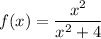
To differentiate the given function, use the quotient rule and the power rule of differentiation.

`\boxed{\begin{minipage}{5.4 cm}\underline{Quotient Rule of Differentiation}\\\\If $y=(u)/(v)$ then:\\\\$\frac{\text{d}y}{\text{d}x}=\frac{v \frac{\text{d}u}{\text{d}x}-u\frac{\text{d}v}{\text{d}x}}{v^2}$\\\end{minipage}}`

`\boxed{\begin{minipage}{5.4 cm}\underline{Power Rule of Differentiation}\\\\If $y=x^n$, then $\frac{\text{d}y}{\text{d}x}=nx^(n-1)$\\\end{minipage}}`

`\boxed{\begin{minipage}{5.4cm}\underline{Differentiating a constant}\\\\If $y=a$, then $\frac{\text{d}y}{\text{d}x}=0$\\\end{minipage}}`

`\begin{aligned}\textsf{Let}\;u &= x^2& \implies \frac{\text{d}u}{\text{d}{x}} &=2 \cdot x^((2-1))=2x\\\\\textsf{Let}\;v &=x^2+4& \implies \frac{\text{d}v}{\text{d}{x}} &=2 \cdot x^((2-1))+0=2x\end{aligned}`

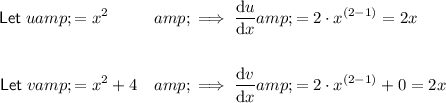
Apply the quotient rule:

`\implies f'(x)=\frac{v \frac{\text{d}u}{\text{d}x}-u\frac{\text{d}v}{\text{d}x}}{v^2}`

`\implies f'(x)=((x^2+4) \cdot 2x-x^2 \cdot 2x)/((x^2+4)^2)`

`\implies f'(x)=(2x(x^2+4)-2x^3)/((x^2+4)^2)`

`\implies f'(x)=(2x^3+8x-2x^3)/((x^2+4)^2)`

`\implies f'(x)=(8x)/((x^2+4)^2)`

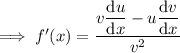
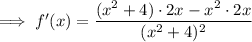
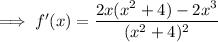
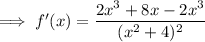
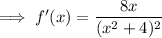
An extremum is a point where a function has a maximum or minimum value. From inspection of the given graph, the minimum point of the function is (0, 0).

To determine the value of the derivative at the minimum point, substitute x = 0 into the differentiated function.

`\begin{aligned}\implies f'(0)&=(8(0))/(((0)^2+4)^2)\\\\&=(0)/((0+4)^2)\\\\&=(0)/((4)^2)\\\\&=(0)/(16)\\\\&=0 \end{aligned}`

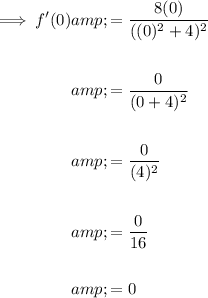
Therefore, the value of the derivative at (0, 0) is zero.