Question

What is the exact value of the trigonometric expression? State your answer in simplified radical form and include all work.

*Please reference included picture for problem. Thank you!

Answer 1

The exact value of the given trigonometric expression is undefined.

Explanation:

Given trigonometric expression:

`(\cos\left((2 \pi)/(3)\right))/(\tan\left(-(7 \pi)/(4)\right))+\csc(\pi)`

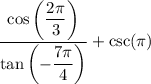
To find the exact value of the given trigonometric expression, begin by finding the exact values of each of the trigonometric functions in the expression

The exact value of cos(2π/3) is:

`\implies \cos\left((2 \pi)/(3)\right)=-(1)/(2)`

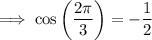
The exact value of tan(-7π/4) is:

`\implies \tan\left(-(7 \pi)/(4)\right)=1`

Since the cosecant function is the reciprocal of the sine function, the exact value of csc(π) is:

`\implies \csc (\pi)=(1)/(\sin(\pi))=(1)/(0)=\textsf{unde\:\!fined}`

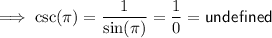
Therefore:

`\begin{aligned}\implies (\cos\left((2 \pi)/(3)\right))/(\tan\left(-(7 \pi)/(4)\right))+\csc(\pi)&=(-(1)/(2))/(1)+(1)/(0)\\&=-(1)/(2)+(1)/(0)\\\\&=\textsf{unde\:\!fined}\end{aligned}`