Question

What is the equation of the circle in the standard (x, y) coordinate plane that has a radius of 4 units and the same center as the circle determined by x^2 + y^2 - 6y + 4=0?

A. x² + y^2 = -4
B. (x+3)^2 + y^2 = 16
C. (x-3)^2 + y^2 = 16
D. x^2 + (y+3)^2 = 16
E. x^2 + (y-3)^2 = 16

Answer 1

To find:-

• The equation of circle which has a radius of 4units and same centre as determined by x² + y² - 6y + 4 = 0.

Answer:-

The given equation of the circle is ,

`\implies x^2+y^2-6y + 4 = 0 \\`

Firstly complete the square for y in LHS of the equation as ,

`\implies x^2 + y^2 -2(3)y + 4 = 0 \\`

Add and subtract 3² ,

`\implies x^2 +\{ y^2 - 2(3)(y) + 3^2 \} -3^2 + 4 = 0 \\`

The term inside the curly brackets is in the form of a²-2ab+b² , which is the whole square of "a-b" . So we may rewrite it as ,

`\implies x^2 + (y-3)^2 -9 + 4 = 0 \\`

`\implies x^2 + (y-3)^2 - 5 = 0 \\`

`\implies x^2 + (y-3)^2 = 5\\`

can be further rewritten as,

`\implies (x-0)^2 + (y-3)^2 = \sqrt5^2\\`

now recall the standard equation of circle which is ,

`\implies (x-h)^2 + (y-k)^2 = r^2 \\`

where,

• (h,k) is the centre.
• r is the radius.

So on comparing to the standard form, we have;

`\implies \rm{Centre} = (0,3)\\`

Now we are given that the radius of second circle is 4units . On substituting the respective values, again in the standard equation of circle, we get;

`\implies (x-h)^2 + (y-k)^2 = r^2 \\`

`\implies (x-0)^2 + (y-3)^2 = 4^2 \\`

`\implies \underline{\underline{\red{ x^2 + (y-3)^2 = 16}}}\\`

and we are done!

Answer 2

E. x² + (y - 3)² = 16

Explanation:

The equation of a circle in the standard (x, y) coordinate plane with center (h, k) and radius r is given by:

`\boxed{(x - h)^2 + (y - k)^2 = r^2}`

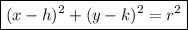
To find the equation of the circle with a radius of 4 units and the same center as the circle determined by x² + y² - 6y + 4 = 0, we need to first write the equation of the second circle in the standard form.

We can complete the square for y to rewrite this equation in standard form. To do this move the constant to the right side of the equation:

`\implies x^2 + y^2 - 6y + 4 = 0`

`\implies x^2 + y^2 - 6y = -4`

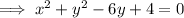
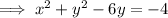
Add the square of half the coefficient of the term in y to both sides of the equation:

`\implies x^2 + y^2 - 6y +\left((-6)/(2)\right)^2= -4+\left((-6)/(2)\right)^2`

`\implies x^2 + y^2 - 6y +9= -4+9`

`\implies x^2 + y^2 - 6y +9=5`

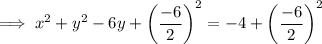
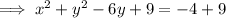
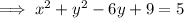
Factor the perfect square trinomial in y:

`\implies x^2+(y-3)^2=5`

`\implies (x-0)^2 + (y-3)^2=5`

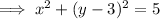
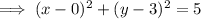
So the center of this circle is (0, 3) and its radius is √5 units.

Since the new circle has the same center, its center is also (0, 3).

We know its radius is 4 units, so we can write the equation of the new circle as:

`\implies (x - 0)^2 + (y - 3)^2 = 4^2`

`\implies x^2 + (y - 3)^2 = 16`

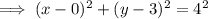
Therefore, the equation of the circle in the standard (x, y) coordinate plane with a radius of 4 units and the same center as the circle determined by x² + y² - 6y + 4 = 0 is x² + (y - 3)² = 16.