Question

An engineer is designing the runway for an airport. Of the plane that will use the airport, the lowest acceleration rate is likely to be 3 m/s2 . The takeoff speed for this plane will be 65 m/s. Assuming this minimum acceleration, what is the minimum allowed length for the runway?

Answer 1

Approximately
`705\; {\rm m}`.

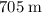Step-by-step explanation:

Let
`x` denote the distance travelled before the plane takes off.

Let
`u` denote the initial velocity of the plane, and let
`v` denote the velocity of the plane when it takes off. It is given that the takeoff speed is
`v = 65\; {\rm m\cdot s^(-1)}`. Assuming that the plane was initially stationary, initial velocity would be
`u = 0\; {\rm m\cdot s^(-1)}`.

It is given that the acceleration of the plane would be
`a = 3\; {\rm m\cdot s^(-2)}`.

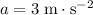Since acceleration is constant, apply the SUVAT equation
`x = (v^(2) - u^(2)) / (2\, a)` to find the value of
`x`:

`\begin{aligned} x &= (v^(2) - u^(2))/(2\, a) \\ &= ((65)^(2) - (0)^(2))/(2\, (3))\; {\rm m} \\ &\approx 705\; {\rm m}\end{aligned}`.

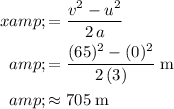(Rounded up.)

Hence, the length of the runway should be at least
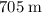`705\; {\rm m}`.