Question

Ciara has $4,300 in savings. If she deposits the money into a long-term savings account with 2.13% APY and monthly compounding, what will the accrued value of her account be in five years?

Answer 1

The accrued value of Ciara's account after five years will be approximately $4,911.46.

Step-by-step explanation:

To find the accrued value of Ciara's account after five years, we can use the formula for compound interest:

`A = P(1 + r/n)^(^n^t^)`

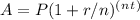
Where:

• A is the accrued value
• P is the principal amount (initial deposit)
• r is the annual interest rate (expressed as a decimal)
• n is the number of times interest is compounded per year
• t is the number of years

For Ciara's case:

• P = $4,300
• r = 0.0213 (2.13% expressed as a decimal)
• n = 12 (monthly compounding)
• t = 5 years

Substituting these values into the formula, we can calculate the accrued value:

1. A = 4300(1 + 0.0213/12)⁽¹²*⁵⁾
2. A ≈ 4300(1 + 0.001775)⁽⁶⁰⁾
3. A ≈ 4300(1.001775)⁽⁶⁰⁾
4. A ≈ 4300(1.139033)
5. A ≈ $4,911.46

Therefore, the accrued value of Ciara's account after five years will be approximately $4,911.46.