Question

Find the value of x to the nearest tenth.

Answer 1

Answer: "x" is 4.5

Explanation:

first lets find the leg of the first right triangle using the given leg of 6 and the hypoteneuse of 9 using Pythagorean theorem a^2 + b^2 = c^2.

6^2 + b^2 = 9^2

36 + b^2 = 81

subtract 36 from both sides to isolate b

36 - 36 + b^2 = 81 - 36

simplify

b^2 = 45

take square root of both sides

`\sqrt{b^(2) }` =
`√(45)`

b = 6.7

Now we can find x of the 2nd right triangle using the know hypoteneuse of 6.7 and the known leg of 5

a^2 + b^2 = c^2

5^2 = b^2 = 6.7^2

25 + b^2 = 44.9

subtract 25 from both sides to isolate b

25 - 25 + b^2 = 44.9 - 25

b^2 = 19.9

take square root of both sides

`√(b^2)` =
`√(19.9)`

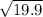
b= 4.5

so your answer to what is "x" is 4.5