1 ]
Given:-


To find:-

Solution:-

now , put the value of x = -3 in equation


or

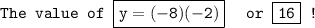

━━━━━━━━━━━━━━━━━━━━━━━━━━━━
2 ]
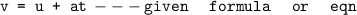
a ) ----»
Given:-



To find:-

Solution:-

now , put the given value in equation



____________________________________
b )
Given:-



To find:-

Solution:-

put the given value in equation





____________________________________
c )
Given:-



To find:-

Solution:-

now , put the given value in equation






━━━━━━━━━━━━━━━━━━━━━━━━━━━
3 ]
Given:-

To find:-

By using given formula:-

Solution:-




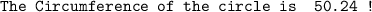

━━━━━━━━━━━━━━━━━━━━━━━━━━━
4 ]
Given:-


To find:-

By using formula:-

Solution:-



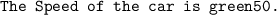
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
hope it helps⸙