Question

Solve the Linear Programming Problem.

Maximize z = 5x+5y
subject to 10x +6y ≥ 150
13x - 13y ≥ - 13
x + y ≤ 45
x ≥ 0
y ≥ 0

What is the maximum value of​ z? Select the correct choice below​ and, if​ necessary, fill in the answer box to complete your choice.
A. z = ___
B. There is no maximum value of z.

At what corner​ point(s) does the maximum value of z​ occur? Select the correct choice below​ and, if​ necessary, fill in the answer box to complete your choice


A. The maximum value of z occurs only at the​ point(s) ___
​(Type an ordered pair. Use a comma to separate answers as​ needed.)
B. The maximum value of z occurs at the points ___
​(Type an ordered pair. Use a comma to separate answers as​ needed.)
C. There is no maximum value of z.

Answer 1

A. z = 225

B. The maximum value of z occurs at the points (22, 23) and (45, 0).

Explanation:

To solve the linear programming problem using graphical methods, we need to graph the inequalities and find the feasible region. Then, we can identify the corner points of the feasible region and evaluate the objective function at each of these points to determine the maximum value of z.

Objective function: z = 5x + 5y

Constraints:

• 10x + 6y ≥ 150
• 13x - 13y ≥ -13
• x + y ≤ 45
• x ≥ 0
• y ≥ 0

Graph each of these inequalities by first plotting the corresponding boundary line, and then shading in the appropriate region.

Rearrange the first three inequalities to isolate y:

`\boxed{\begin{aligned}10x +6y &\geq 150\\6y &\geq-10x+ 150\\y &\geq -(5)/(3)x+25\\\end{aligned}}`
`\boxed{\begin{aligned}13x - 13y &\geq - 13\\x -y &\geq -1\\ x +1 &\geq y\\ y &\leq x+1\end{aligned}}`
`\boxed{\begin{aligned}x + y &\leq 45\\y&\leq-x+45\\\phantom{w}\\\phantom{w}\end{aligned}}`

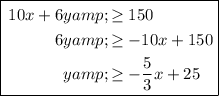
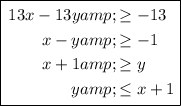
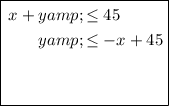
Graph the inequalities.

• If the inequality sign is ≥, draw a solid line and shade above the line.
• If the inequality sign is ≤, draw a solid line and shade below the line.

The feasible region is the region that is shaded by all of the inequalities.

Please see the attached graph.

A bounded feasible region may be enclosed in a circle and will have both a maximum value and a minimum value for the objective function. Therefore, as the feasible region for the given constraints is bounded, there is a maximum value of z.

The feasible region is bounded by the corner points:

• (9, 10)
• (22, 23)
• (45, 0)
• (15, 0)

Evaluate the objective function z = 5x + 5y at each of these corner points:

Point (9, 10): z = 5(9) + 5(10) = 95

Point (22, 23): z = 5(22) + 5(23) =225

Point (45, 0): z = 5(45) + 5(0) = 225

Point (15, 0): z = 5(15) + 5(0) = 75

Therefore, the maximum value of z is 225, which occurs at the corner points (22, 23) and (45, 0).