Question

Can someone help me answer this question please??
The exponent say -0.0251t

Answer 1

A)

`s(t)=35+36e^(-0.0251t)\hspace{4em}s(15)=35+36e^(-0.0251(15))\implies s(15)\approx 59.0`

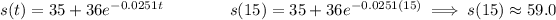
B)

`\displaystyle \lim_(x\to \infty)s(t)\implies \lim_(x\to \infty)35+36e^(-0.0251t)\implies \lim_(x\to \infty)35+ \cfrac{36}{e^(0.0251t)} \\\\[-0.35em] ~\dotfill\\\\ t=99\hspace{5em}\implies 35+\cfrac{36}{e^(0.0251(99))}\implies 35+\cfrac{36}{e^(2.4849)} \\\\\\ t=9999\hspace{5em}\implies 35+\cfrac{36}{e^(0.0251(9999))}~ \approx ~ 35+\cfrac{36}{e^(250.97)} \\\\\\ t=9999999\hspace{5em}\implies 35+\cfrac{36}{e^(0.0251(9999999))}~ \approx ~ 35+\cfrac{36}{e^(250999.97)}`

so let's notice, as "t" increases, denominator with the 36 above is increasing, as "t" gets larger and larger that denominator is become huge whilst the numerator is not moving, so whenever we have an ever increasing denominator with an stagnant numerator the fraction as a whole is going to "0" and we're leftout only with our 35. So we can say

`\displaystyle \lim_(x\to \infty)s(t)\implies \lim_(x\to \infty)35+36e^(-0.0251t)\implies \lim_(x\to \infty)35+ \cfrac{36}{e^(0.0251t)}~~ = ~~\text{\LARGE 35}`

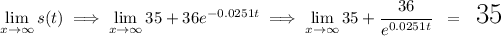
C)

Check the picture below.

D)

well, check in the picture below, in the brown region the line is less flat than in the green region, so the temperature is dropping faster in the first 10 minutes.