Both equations represent the same line, so **infinitely many solutions** exist, expressed by the single equation: **y = -2x + 3**.
Let's solve the system of equations:
y=-2x+3
x=

We can solve the system of equations by elimination.
Steps to solve:
Rearrange terms in standard form:
y+2x=3
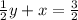
Eliminate y:
Multiply the top equation by
 and add it to the bottom equation:
and add it to the bottom equation:

Conclusion:
Since the result is 0=0, the lines coincide and represent the same line. Therefore, there are infinitely many solutions.
