After reflecting square ABCD on both the x-axis and y-axis, the vertices of square A'B'C'D' will have coordinates A'(−2,−4), B'(−2,−11), C'(−7,−11), and D'(−7,−4), which corresponds to Option A.
To find the coordinates of the vertices for square (A'B'C'D') after reflecting square (ABCD) over the x-axis and the y-axis:
For x-axis reflection, the y-coordinate is negated, and for y-axis reflection, the x-coordinate is negated.
1. X-axis reflection:
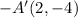
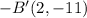
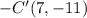
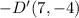
2. Y-axis reflection:
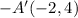
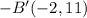
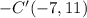
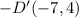
Comparing these results with the given options:
- Option A matches the coordinates after both reflections.
- Option B does not match the coordinates after the y-axis reflection.
Therefore, the correct answer is Option A: Square
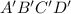 has vertices
has vertices
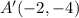 ,
,
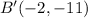 ,
,
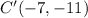 , and
, and
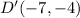 .
.