Question

Which of the following expressions is equivalent to the one shown below?

2log2^25-2log2^5+log2^3

A. 2log2^23
B. log2^75
C. 2log2^15
D. log2^43

Answer 1

B.
`log_(2)(75)`

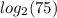
Explanation:

We can solve this problem by condensing the long log expression using three rules of logs:

• The product rule,
• the quotient rule,
• and the power rule.

----------------------------------------------------------------------------------------------------------The product rule of logs:

The product rule of logs says that:

• The logarithm of the product of two numbers is equal to the sum of the logarithms of the individual numbers.

`log_(b)(mn)=log_(b)(m)+log_(b)(n)`

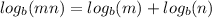
The quotient rule of logs:

The quotient rule of logs says that:

• The logarithm of the quotient of two numbers is equal to the difference of the logarithms of the individual numbers.

`log_(b)((m)/(n))=log_(b)(m)-log_(b)(n)`

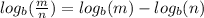
The power rule of logs:

The power rule of logs says that:

• The logarithm of a number raised to an exponent is equal to the exponent multiplied by the logarithm of the base.

`log_(b)(m^n)=n*log_(b)(m)`

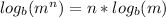
Condensing the large log expression:

Now, we can condense the large log expression using the following steps:

Step 1: Apply the quotient rule of logs and simplify::

`2*log_(2) (25)-2*log_(2)(5)+log_(2)(3)\\\\2*log_(2)((25)/(5))+log_(2)(3)\\ \\2*log_(2)(5)+log_(2)(3)`

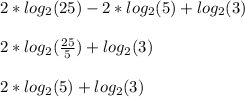
Step 2: Apply the power rule of logs and simplify:

`log_(2)(5^2)+log_(2)(3)\\ \\ log_(2)(25)+log_(2)(3)`

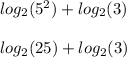
Step 3: Apply the product rule of logs and simplify:

`log_(2)(25*3)\\\\log_(2)(75)`

Therefore, B.
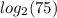`log_(2)(75)` is equivalent to
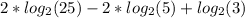`2*log_(2) (25)-2*log_(2)(5)+log_(2)(3)`.

Answer 2

B. log₂75

Explanation:

You want to know the expression equivalent to 2log₂25 -2log₂5 +log₂3.

Rules of logarithms

The relevant rules of logarithms are ...

log(a^b) = b·log(a)
log(ab) = log(a) +log(b)

Application

These rules let us combine the terms of the given expression.

`2\log_225-2\log_25+\log_23\\\\=2\log_25^2-2\log_25+\log_23\\\\=4\log_25-2\log_25+\log_23\\\\=2\log_25+\log_23=\log_2(5^2\cdot3)\\\\=\boxed{\log_275}\qquad\text{matches choice B}`

<95141404393>