Question

What is the 14th partial sum of 2,000 – 1,000 + 500 – 250 + …? Round your answer to the thousandths place.

Answer 1

The 14th partial sum of the series 2,000 – 1,000 + 500 – 250 + … is 286.377 when rounded to the thousandths place.

In this alternating series, each term is half of the previous term, with the first term being 2,000. To find the 14th partial sum, we can use the formula for the sum of a geometric series:

`S_(n) = a(1-r^(n) )/(1-r)`

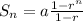
where:

a is the first term (2,000),

r is the common ratio (0.5),

n is the number of terms (14).

Plugging in these values, we get:

`S_(14) = 2000(1-0.5^(14) )/(1-0.5)`

Calculating this expression gives us the 14th partial sum, which is approximately 286.377 when rounded to the thousandths place.