Question

Given Log_a+3(7)<0 need to find the interval of a

Answer 1

-3 < a < -2

(-3, -2)

Explanation:

Given logarithmic inequality:

`\log_(a+3)(7) < 0`

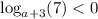
For a logarithm to be negative, the base must be between 0 and 1.

Therefore, if the base of the given logarithm is (a + 3), then for the logarithm to be negative:

`0 < a+3 < 1`

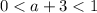
Solve both inequalities:

`\begin{aligned}0 & < a+3\\-3& < a\\a& > -3\end{aligned}`

`\begin{aligned}a+3& < 1\\a& < -2\end{aligned}`

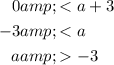
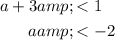
Combine the solutions:

`-3 < a < -2`

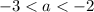
Therefore, for logₐ₊₃(7) < 0, the value of a must be greater than -3 and less than -2, represented in interval notation as (-3, -2).

Additional Notes

For a logarithm to be defined, its base should be positive numbers other than 1.