Question

A rocket is launched from atop a 63 foot cliff with an initial vertical velocity of 92 feet per second. The height

of the rocket r seconds after launch is given by the equation h = - 168 + 92t + 63. Graph the equation to find
second.
out how long after the rocket is launched it will hit the ground. Estimate your answer to the nearest tenth of a second

Answer 1

The rocket needs a time of approximately 6.40 seconds to hit the ground.

How to determine the time needed by the rocket to hit the ground

In this problem we must determine how much time is needed by the rocket to hit the ground. Rocket experiments a free-fall motion, that is, an uniformly accelerated motion due to gravity. Height as a function of time is a quadratic equation of the form:

`h = h_(o) + v_(o)\cdot t + (1)/(2)\cdot g\cdot t^2`

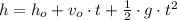
Where:

• 
  `h_o` - Initial height, in feet.
• 
  `v_o` - Initial speed, in feet per second.
• g - Gravitational acceleration, in feet per square second.
• t - Time, in seconds.
• h - Height, in feet.

Now we proceed to determine the time needed by the rocket by graphic approach. By direct inspection, the time needed by the rocket is approximately 6.40 seconds.