Answer:
Approximately
 at
at
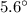 below the horizon.
below the horizon.
- Horizontal component of velocity:
 .
. - Vertical component of velocity:
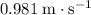 (downwards.)
(downwards.)
(Assumption: air resistance on the ball is negligible;
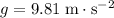 .)
.)
Step-by-step explanation:
Assume that the air resistance on the ball is negligible. The horizontal component of the velocity of the ball would stay the same at
 until the ball reaches the ground.
until the ball reaches the ground.
On the other hand, the vertical component of the ball would increase (downwards) at a rate of
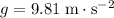 (where
(where
 is the acceleration due to gravity.) In
is the acceleration due to gravity.) In
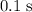 , the vertical component of the velocity of this ball would have increased by
, the vertical component of the velocity of this ball would have increased by
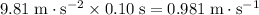 .
.
However, right after the ball rolled off the edge of the table, the vertical component of the velocity of this ball was
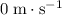 . Hence,
. Hence,
 after the ball rolled off the table, the vertical component of the velocity of this ball would be
after the ball rolled off the table, the vertical component of the velocity of this ball would be
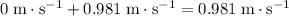 .
.
Calculate the magnitude of the velocity of this ball. Let
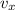 and
and
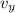 and denote the horizontal and vertical component of the velocity of this ball, respectively. The magnitude of the velocity of this ball would be
and denote the horizontal and vertical component of the velocity of this ball, respectively. The magnitude of the velocity of this ball would be
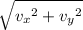 .
.
At
 after the ball rolled off the table,
after the ball rolled off the table,
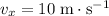 while
while
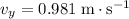 . Calculate the magnitude of the velocity of the ball at this moment:
. Calculate the magnitude of the velocity of the ball at this moment:
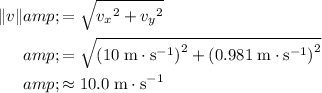 .
.
Calculate the angle between the horizon and the velocity of the ball (a vector) at that moment. Let
 denote that angle.
denote that angle.
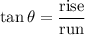 .
.
For the vector representing the velocity of this ball:
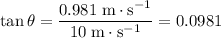 .
.
Calculate the size of this angle:
 .
.
Notice that the vertical component of the velocity of this ball at that moment points downwards (towards the ground.) Hence, the corresponding velocity should point below the horizon.