Question

The sequence 6,12,24,48... shows the number of pushups Kendall did each week, starting with her first week of exercising. a) What is the recursive rule for the sequence? b) What is the iterative rule for the sequence?

Answer 1

Answer for part a) is
`\begin{cases}a_1 = 6\\a_n = 2*a_(n-1) \ \text{ where } n \ge 2\end{cases}`

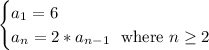
Answer for part b) is
`a_n = 6(2)^(n-1)`

-------------------------------------------------------------------------

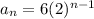
Explanation for Part a)

The recursive rule is

`\begin{cases}a_1 = 6\\a_n = 2*a_(n-1) \ \text{ where } n \ge 2\end{cases}`

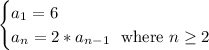
The small number floating slightly below the 'a' is the index.

`a_1` = first term,
`a_2` = second term,
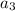`a_3` = third term, etc

The first term is 6, so that's our first row.

The second row is the recursive step. It's the recipe we follow to generate each new term. That recipe is "Multiply 2 with the previous term to get the next term", in other words "double each term to get the next term".

`a_n` = nth term

`a_(n-1)` = term just before the nth term

-------------------------------------------------------------------------

Explanation for Part b)

The sequence 6,12,24,48,... is geometric. We can confirm this by dividing each term by its previous term.

12/6 = 2

24/12 = 2

48/24 = 2

We get the same common ratio each time. That common ratio is r = 2.

The starting term is a = 6

The nth term of the geometric sequence is
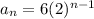`a_n = 6(2)^(n-1)` where n = 1 is the starting value and n is a whole number. The general template for the nth term of a geometric sequence is
`a_n = a(r)^(n-1)`

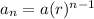
Let's check this claim. I'll plug in n = 3

`a_n = 6(2)^(n-1)\\\\a_3 = 6(2)^(3-1)\\\\a_3 = 6(2)^(2)\\\\a_3 = 6(4)\\\\a_3 = 24\\\\`

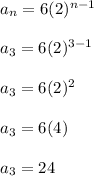
The third term is indeed 24, so this helps partially verify the answer. I'll let the student verify the other values of n.