Question

The half-life of carbon-14 is 5,730 years. Suppose a fossil is found with 20 percent as much of its carbon-14 as compared to a living sample. How old is the fossil?

a
1,331 years
b
32,346 years
c
3,235 years
d
13,307 years

Answer 1

The age of the fossil is 13, 408 years

Half-life is the time required for a substance to decrease or decay by half of its initial quantity.

The half life of carbon-14 is 5730 years

N(t) = 20/100 × N(o)

where N(t) is the found value and N(o) is the intial value.

N(t) = 0.2N(o)

N(t) = N(o) e⁻ˣⁿ

where n is the number of years and x is the decay constant

decay constant = 0.693/half life

decay constant = 0.693/ 5730

= 0.00012

`e { }^( - 0.00012t) = 0.2`

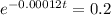
-0.00012t = ln0.2

-0.00012t = -1.609

t = -1.609/-0.00012

t = 13408 ( nearest years)