Question

(1,4), (2, 8), (3, 16), (4, 32) Parte A: ¿Estos datos modelan una función lineal o una función exponencial? Explica tu respuesta. Parte B: Escribe una función para representar los datos. Muestra tu trabajo. Parte C: Determina la tasa de cambio promedio entre la estación 2 y la estación 4. Muestra tu trabajo. ​

Answer 1

A. The given data model represents an exponential function.

B. A function to represent the data is
`f(x) = 4(2)^x`.

C. The average rate of change between station 2 and station 4 is 12.

Part A.

In Mathematics, a linear function has constant rate of change (slope). Based on the data set, the slope can be calculated as follows;

`Slope (m)=(y_2-y_1)/(x_2-x_1)`

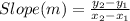
Slope (m) = (8 - 4)/(2 - 1) = (16 - 8)/(3 - 2)

Slope (m) = 4 ≠ 8

An exponential function has a common ratio and this can be calculated as follows;

Common ratio =
`(y_2)/(y_1)`

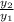
Common ratio = 8/4 = 16/8 = 32/16

Common ratio = 2.

Part B.

Since the first term is 4 and the common ratio is 2, an exponential function that models the data set can be written as follows;

`f(x) = a(b)^x\\\\f(x) = 4(2)^x`

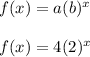
Part C.

Next, we would determine the average rate of change of the function f(x) over the interval [2, 4] by using this formula:

Average rate of change =
`(f(b) - f(a))/((b - a))`

a = 2; f(a) = 8

b = 4; f(b) = 32

By substituting the given parameters into the average rate of change formula, we have the following;

Average rate of change = (32 - 8)/(4 - 2)

Average rate of change = 24/2

Average rate of change = 12.

Complete Question:

(1,4), (2, 8), (3, 16), (4, 32)

Part A: Do these data model represent a linear function or an exponential function? Explain your answer.

Part B: Write a function to represent the data. Show your work.

Part C: Determine the average rate of change between station 2 and station 4. Show your work.​