Question

A car accelerates uniformly from rest and reaches a speed of 24.8 m/s in 6.7 s.The diameter of a tire is 70.2.Find the number of revolutions the tire makes during this motion assuming no slipping

Answer 1

37.6 revs

Note: The diameter of the tire was NOT GIVEN specified units. It was ASSUMED to be in CENTIMETERS.

Step-by-step explanation:

To solve this problem, we first need to determine the distance traveled by the car during its acceleration, then calculate the number of tire revolutions based on this distance.

Given:

• v₀ = 0 m/s
• v_f = 24.8 m/s
• t = 6.7 s
• d = 70.2 cm

`\hrulefill`

Determining the Distance Traveled
`\hrulefill`

The car accelerates uniformly from rest, meaning we can use a kinematic equation for uniformly accelerated motion. Here are the four kinematic equations:

`\boxed{\left\begin{array}{ccc}\text{\underline{The 4 Kinematic Equations:}}\\\\1. \ \vec v_f=\vec v_0+\vec at\\\\2. \ \Delta \vec x=(1)/(2)(\vec v_f+\vec v_0)t\\\\3. \ \Delta \vec x=\vec v_0t+(1)/(2)\vec at^2\\\\ 4. \ \vec v_f^2=\vec v_0^2+2\vec a \Delta \vec x \end{array}\right}`

Lets use equation (2) to determine the distance traveled (Δx):

`\Longrightarrow \Delta \vec x = (1)/(2)(\vec v_f+\vec v_0)t\\\\\\\\\Longrightarrow \Delta \vec x = (1)/(2)(24.8 \text{ m/s$^2$}+0 \text{ m/s$^2$})(6.7 \text{ s})\\\\\\\\\therefore \Delta \vec x \approx 83.1 \text{ m}`

`\hrulefill`

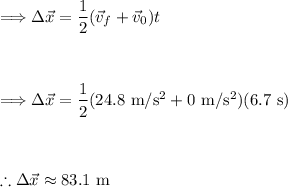
Calculating the Number of Revolutions
`\hrulefill`

We can now find the number of revolutions. The circumference of the tire, which is the distance it covers in one revolution, is given by:

`C = 2 \pi r=\pi d`

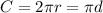
Let's find the circumference of the tire:

`\Longrightarrow C= \pi \left(70.2 \text{ cm} * \frac{1 \text{ m}}{100 \text{ cm}}\right)\\\\\\\\\therefore C \approx 2.21 \text{ m}`

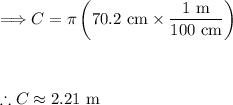
Knowing the circumference, we can calculate the number of revolutions as:

`\text{Revolutions $=$ $\frac{\text{Distance Traveled}}{\text{Circumference of Tire}}$}\\\\\\\\\Longrightarrow \text{Revs}=\frac{83.1 \text{ m}}{2.21 \text{ m}}\\\\\\\\\therefore \text{Revs} \approx \boxed{37.6}`

The tire makes approximately 37.6 revolutions during this motion.