Question

Help needed right away

Answer 1

In congruent triangles
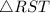`\( \triangle RST \)` and ,
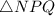`\( \triangle NPQ \)` corresponding angles are equal. Thus, if
`\( \angle T \)` corresponds to
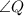`\( \angle Q \)`, they are congruent.

In geometry, when two triangles are congruent, it means that their corresponding angles and sides are equal. Given that
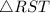`\( \triangle RST \)` is congruent to
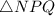`\( \triangle NPQ \)`, we can denote this congruence as
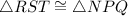`\( \triangle RST \cong \triangle NPQ \)`. According to the corresponding parts of congruent triangles (CPCT) theorem, corresponding angles of congruent triangles are congruent.

Therefore, if
`\( \angle T \)` is a corresponding angle in
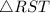`\( \triangle RST \)` , then it is congruent to its corresponding angle in
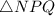`\( \triangle NPQ \)`. This can be expressed as
`\( \angle T \cong \angle Q \)`.

So, in conclusion, if
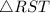`\( \triangle RST \)` is congruent to
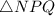`\( \triangle NPQ \)`, then
`\( \angle T \)` is congruent to
`\(\angle Q \)`