Question

In a survey of a community, it was found that 55%

like summer season, 20% like winter season, 40%
don't like both seasons and 750 like both seasons. By
using Venn diagram, find the number of people who
like winter season.​

Answer 1

The number of people who like winter season is 1000.

Explanation:

Event event correspond to a set in the Venn diagram, and we use it to find the percentages.

I am going to say that:

Event A: Like summer season

Event B: Like winter season.

55% like summer season

This means that
`P(A) = 0.55`

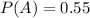
20% like winter season

This means that
`P(B) = 0.2`

40% don't like both seasons

This means that 100% - 40% = 60% like at least one, which means that
`P(A \cup B) = 0.6`

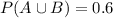
Proportion who like both:

This is
`P(A \cap B)`. The measures are related by the following equation:

`P(A \cup B) = P(A) + P(B) - P(A \cap B)`

`P(A \cap B) = P(A) + P(B) - P(A \cup B)`

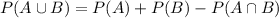
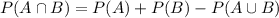
Using what we have

`P(A \cap B) = 0.55 + 0.2 - 0.6 = 0.15`

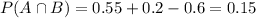
750 like both seasons.

This is 15% of the sample. So the total number of people is t, for which:

`0.15t = 750`

`t = (750)/(0.15)`

`t = 5000`

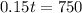
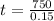
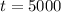
20% like winter season

Out of 5000. So

0.2*5000 = 1000

The number of people who like winter season is 1000.