Question

Please someone please just answer my questions

Answer 1

The value of the length x must be 1.

x = 1.

How to find the value of x?

Notice that the vertex in the top is common to both triangles, so both triangles have an equal angle there.

if we look at the smaller triangle, we can write:

cos(angle) = x/2

(because in that angle, x is the adjacent cathetus)

For the larger triangle we have an adjacent cathetus of 2 units and an hypotenuse of (x + 3), then we can also write:

cos(angle) =2/(x + 3)

Then we can write the equation:

x/2 = 2/(x + 3)

Now we can solve this for x:

x*(x + 3) = 2*2

x² + 3x = 4

x² + 3x - 4 = 0

now we can use the quadratic formula to get the solutions:

`x = (-3 \pm √(3^2 - 4*1*-4) )/(2) \\\\x = (-3 \pm 5 )/(2)`

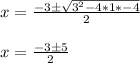
We only care for the positive solution (because x is a length) then:

x = (-3 + 5)/2 = 1