Question

Out of some students appeared in an examination,

80% passed in English, 75% passed in Science and
5% failed in both subjects. If 300 of them were
passed in both subjects, how many students were
appeared in the examination? Find it by using a
Venn-diagram
(Ans: 500​

Answer 1

500 students appeared in the examination.

Explanation:

Each event represents a set in the Venn diagram, and we use it to find the desired values.

I am going to say that:

Event A: Passed in English.

Event B: Passed in Science.

80% passed in English

This means that
`P(A) = 0.8`.

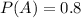75% passed in Science

This means that
`P(B) = 0.75`

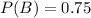
5% failed in both subjects.

This means that 100% - 5% = 95% passed at least one of these subjects, so
`P(A \cup B) = 0.95`.

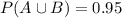Proportion that passed both subjects:

This is
`P(A \cap B)`

These percentages are related by the following equation:

`P(A \cap B) = P(A) + P(B) - P(A \cup B)`

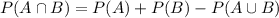
So

`P(A \cap B) = 0.8 + 0.75 - 0.95 = 0.6`

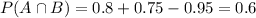
Number of students in class:

60% of the total number t passed both subjects. This is equals to 300. So

`0.6t = 300`

`t = (300)/(0.6)`

`t = 500`

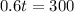
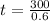
500 students appeared in the examination.