Question

The green triangle is a dilation of the red triangle with a scale factor of s=13 and the center of dilation is at the point (4,2)

What are the coordinates of Point C'? C'(___,____)

What are the coordinates of Point A? A(____,____)

Answer 1

Given:

The red figure dilated with a scale factor of
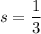`s=(1)/(3)` and the center of dilation is at the point (4,2) to get the green figure.

To find:

The coordinates of C' and A.

Solution:

If a figure is dilated with a scale factor k and the center of dilation is at the point (a,b), then

`(x,y)\to (k(x-a)+a,k(y-b)+b)`

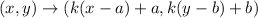
In given problem, the scale factor is
`(1)/(3)` and the center of dilation is at (4,2).

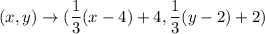`(x,y)\to ((1)/(3)(x-4)+4,(1)/(3)(y-2)+2)` ...(i)

Let the vertices of red triangle are A(m,n), B(10,14) and C(-2,11).

Using (i), we get

`C(-2,11)\to C'((1)/(3)(-2-4)+4,(1)/(3)(11-2)+2)`

`C(-2,11)\to C'((1)/(3)(-6)+4,(1)/(3)(9)+2)`

`C(-2,11)\to C'(-2+4,3+2)`

`C(-2,11)\to C'(2,5)`

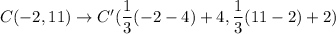
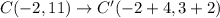
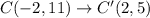
Therefore, the coordinates of Point C' are C'(2,5).

We assumed that point A is A(m,n).

Using (i), we get

`A(m,n)\to A'((1)/(3)(m-4)+4,(1)/(3)(n-2)+2)`

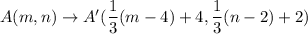
From the given figure it is clear that the image of point A is (8,4).

`A'((1)/(3)(m-4)+4,(1)/(3)(n-2)+2)=A'(8,4)`

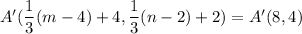
On comparing both sides, we get

`(1)/(3)(m-4)+4=8`

`(1)/(3)(m-4)=8-4`

`(m-4)=3(4)`

`m=12+4`

`m=16`

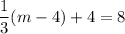
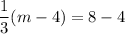
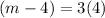
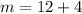
And,

`(1)/(3)(n-2)+2=4`

`(1)/(3)(n-2)=4-2`

`(n-2)=3(2)`

`n=6+2`

`n=8`

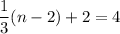
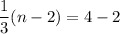
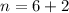
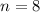
Therefore, the coordinates of point A are (16,8).