Question

A college student is deciding how many hours to work at a part time job(x) and how many hours to work at an internship (y). The job pays $24 and hour, and the internship pays $12 an hour. The student needs to work less than 15 hours a week but needs to earn at least $240 a week to pay expenses. Write 2 systems of inequalities to represent all the combinations of number of hours the student can work at the job and internship

Answer 1

`\begin{cases} x+y < 15\\24x+12y \geq 240 \end{cases}`

`\begin{cases} x+y < 15\\2x+y \geq 20 \end{cases}`

Explanation:

Part-time job

• Let x be the number of hours worked.
• $24 = pay per hour.

Internship

• Let y be the number of hours worked.
• $12 = pay per hour.

The student needs to work less than 15 hours a week:

`\implies x+y < 15`

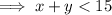
The student needs to earn at least $240 a week:

`\implies 24x+12y \geq 240`

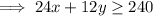
Therefore, the system of inequalities is:

`\begin{cases} x+y < 15\\24x+12y \geq 240 \end{cases}`

The second inequality can be simplified by dividing each term by 12:

`\implies (24x)/(12)+(12y)/(12) \geq (240)/(12)`

`\implies 2x+y \geq 20`

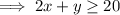
Therefore, a second system of inequalities is:

`\begin{cases} x+y < 15\\2x+y \geq 20 \end{cases}`

To solve the system of equalities, graph both inequalities and shade the overlapping region.

Any (x, y) point in the overlapping region is a solution to the system of inequalities.

Answer 2

• x + y < 15
• 2x + y ≥ 20

-------------------------------

Total hours worked is x + y.

Earning from the part time job is 24x, from the internship is 12y.

Inequality for the number of hours:

• x + y < 15

Inequality for the earning:

• 24x + 12y ≥ 240

This can be simplified by dividing all terms by 12:

• 2x + y ≥ 20