Question

Find the distance between the two given points. O(-3,-2) and P(-3,4)​

Answer 1

`\boxed {\boxed {\sf d= 6}}`

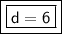
Explanation:

Distance can be found using this formula:

`d=\sqrt {(x_2-x_1)^2+(y_2-y_1)^2`

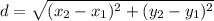
Where (x₁, y₁) and (x₂, y₂) are the points.

We are given the points O (-3, -2) and P(-3,4). Therefore,

`x_1= -3 \\y_1= -2 \\x_2= -3 \\y_2=4`

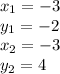
Substitute the values into the formula.

`d=\sqrt {(-3--3)^2+(4--2)^2`

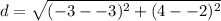
Solve according to PEMDAS: Parentheses, Exponents, Multiplication, Division, Addition and Subtraction.

Solve inside the parentheses first.

• (-3--3)= -3+3=0
• (4--2)= 4+2=6

`d= \sqrt {(0)^2+ (6)^2}`

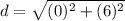
Solve the exponents.

• (0)²= 0*0=0
• (6)²= 6*6=36

`d=\sqrt {0+36`

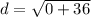
Add.

`d= \sqrt {36`

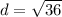
Take the square root.

`d=6`

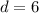
The distance is 6.