From
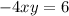 ,
,
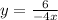 . Substituting into \(-5x - y = 21\) creates a quadratic equation. Solutions:
. Substituting into \(-5x - y = 21\) creates a quadratic equation. Solutions:
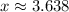 with
with
 and
and
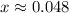 with
with
 .
.
Given equations:
1.
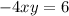
2.
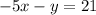
From equation (1), isolate \(y\) in terms of \(x\):
![\[ y = (6)/(-4x) \]](https://img.qammunity.org/2024/formulas/mathematics/college/1xcir6sus3pk5d70b7tu68iuv5rcur2pal.png)
Now substitute this expression for \(y\) into equation (2):
![\[ -5x - (6)/(-4x) = 21 \]](https://img.qammunity.org/2024/formulas/mathematics/college/leb3dkno5heksr641754x9zcrok08c6j2d.png)
To eliminate the denominator, multiply both sides by \(-4x\):
![\[ -20x^2 + 6 = -84x \]](https://img.qammunity.org/2024/formulas/mathematics/college/busjoejwgvwlffoicq52fojkgqq1ziinfu.png)
Rearrange terms to form a quadratic equation:
![\[ 20x^2 - 84x + 6 = 0 \]](https://img.qammunity.org/2024/formulas/mathematics/college/49u3kp41ammk1nhhds6do92nb0w229w1dn.png)
Apply the quadratic formula:
![\[ x = (-b \pm √(b^2 - 4ac))/(2a) \]](https://img.qammunity.org/2024/formulas/mathematics/college/n2775bpyhr6nkttp819uth89i6m8ha2p28.png)
For the equation
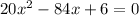 :
:
![\[ a = 20, \, b = -84, \, c = 6 \]](https://img.qammunity.org/2024/formulas/mathematics/college/6dub0s2e619ck8w9exn8zgcx8cht9maiz8.png)
Substitute these values into the quadratic formula:
![\[ x = (84 \pm √((-84)^2 - 4(20)(6)))/(2(20)) \]](https://img.qammunity.org/2024/formulas/mathematics/college/1dgbsnbpvvej8dawobvy5ehylye8tjdgb2.png)
![\[ x = (84 \pm √(7056 - 480))/(40) \]](https://img.qammunity.org/2024/formulas/mathematics/college/kubmn4llthvhpua3127kv24i0o2i89ttor.png)
![\[ x = (84 \pm √(6576))/(40) \]](https://img.qammunity.org/2024/formulas/mathematics/college/ney52sc8f19pkp49ckpze6n9zoet30n8ys.png)
![\[ x = (84 \pm 81.095)/(40) \]](https://img.qammunity.org/2024/formulas/mathematics/college/j6r3ob1ljh1gmtnbsrq2qafksiys37k909.png)
Two possible solutions for \(x\):
![\[ x_1 = (84 + 81.095)/(40) \approx 3.638 \]](https://img.qammunity.org/2024/formulas/mathematics/college/9mupf50bhiu19fgy9ruopwaottdhzyeztz.png)
![\[ x_2 = (84 - 81.095)/(40) \approx 0.048 \]](https://img.qammunity.org/2024/formulas/mathematics/college/4j5m3c8zsqd6koxeoiujtsboprquvip72d.png)
Now substitute these \(x\) values into
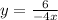 to determine the corresponding values of \(y\):
to determine the corresponding values of \(y\):
For
 :
:
![\[ y_1 = (6)/(-4(3.638)) \approx -0.412 \]](https://img.qammunity.org/2024/formulas/mathematics/college/aknj3ou144wv3n2on9seg4gew1uappptd5.png)
For
 :
:
![\[ y_2 = (6)/(-4(0.048)) \approx -31.25 \]](https://img.qammunity.org/2024/formulas/mathematics/college/7xpbbtrrfv9dhwji9j1v0t9m22al0608i3.png)
Hence, the solutions are approximately
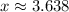 with
with
 and \(x
and \(x
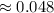 with
with
 .
.
complete the question
"Given the system of equations:
1. \(-4xy = 6\)
2. \(-5x - y = 21\)
Solve the system of equations by substitution. Show the step-by-step process of isolating one variable in terms of the other, substituting the expression, and determining the values of \(x\) and \(y\). Finally, present the solutions for \(x\) and \(y\)."