Answer:
The quadratic polynomial with integer coefficients is
 .
.
Explanation:
Statement is incorrectly written. Correct form is described below:
Find a quadratic polynomial with integer coefficients which has the following real zeros:
 .
.
Let be
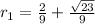 and
and
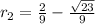 roots of the quadratic function. By Algebra we know that:
roots of the quadratic function. By Algebra we know that:
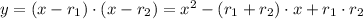 (1)
(1)
Then, the quadratic polynomial is:
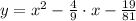

The quadratic polynomial with integer coefficients is
 .
.