Question

First, the triangle is dilated by a scale factor of 1/3 about the origin. Then the triangle is reflected over the x-axis. Finally, the triangle is translated left 3 units and up 2 units.

Answer 1

`((1)/(3)x - 3,-(1)/(3)y+2)`

Both triangles will be similar

Explanation:

See comment for complete question.

Given

Let the coordinates of the triangle be T(x,y)

First transformation: Dilation by 1/3

The new points will be:

`T' = (1)/(3)(x,y)`

`T' = ((1)/(3)x,(1)/(3)y)`

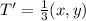
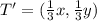
Second: Reflection over the x-axis

When a point (x,y) is reflected over the x-axis, the new point is (x,-y).

So, we have:

`T'' = ((1)/(3)x,-(1)/(3)y)`

Third: Translation 3 units left and 2 units up.

When a point (x,y) is translated b units left and h units up, the new point is (x - b,y+h).

In this case:

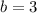`b = 3` and
`h = 2`

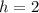
So, we have:

`T''' = ((1)/(3)x - 3,-(1)/(3)y+2)`

Hence, the coordinate of the new triangle will be:
`((1)/(3)x - 3,-(1)/(3)y+2)`

Additionally, both triangles will be similar because all the transformation done are rigid transformations i.e. Dilation, Reflection and Translation