Question

After 5 hours, how far apart are the boats? Label the distance(s) on your drawing from the first problem.

Answer 1

The distance between them is 277.84 m

Explanation:

See comment for complete question.

Given

Boat A:

`Speed = 24mph`

`\angle A = 340^(\circ)`

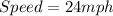
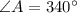
Boat B:

`Speed = 35mph`

`\angle B = 200^(\circ)`

`Time = 5hr`

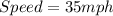
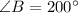
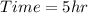
First, we calculate the distance traveled by both boats in 5 hours

`Distance= Speed * Time`

`Boat\ A = 24mph * 5hr = 120m`

`Boat\ B = 35mph * 5hr = 175m`

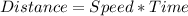
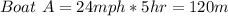
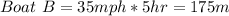
For more clarity, I'll make use of the attached image to represent the system.

From the attachment, we are to calculate distance C, but first we calculate the angle between them.

`\theta = 340^(\circ) - 200^(\circ)`

`\theta = 140^(\circ)`

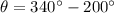
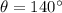
C is then calculated using cosine law:

`C^2 = A^2 + B^2 - 2BC\ Cos\theta`

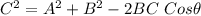
This gives:

`C^2 = 120^2 + 175^2 - 2*120*175\ Cos(140^(\circ))`

`C^2 = 120^2 + 175^2 - 2*120*175*-0.7660`

`C^2 = 14400 + 30625 + 32172`

`C^2 = 77197`

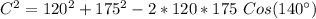
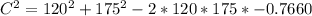
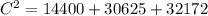
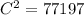
Take square root of both sides:

`C = \sqrt{77197`

`C = 277.84`

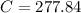
The distance between them is 277.84 m