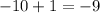Question

The product of two consecutive integers is 90. Find the two integers then check your answer​

Answer 1

9,10 or -10,-9

Explanation:

Let call the first integer n and the second integer n+1 since they are consecutive.

Since the product of the integer is 90 set up this equation

`n * (n + 1)= 90`

`n {}^(2) + n = 90`

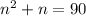
Subtract 90 to get it on the left side

`n {}^(2) + n - 90`

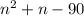
Apply quadratic formula

`- 1 + - \sqrt{ \frac{1 {}^(2) - 4(1)( - 90) }{2(1)} }`

`- 1 + - \sqrt{ (1 - ( - 360)/(2) }`

`- 1 + - \sqrt{ (1 + 360 = 361)/(2) }`

`- 1 + - ( √(361 = ) 19)/(2)`

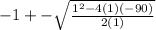
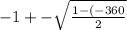
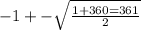
The roots are n= -10 and 9. We can use either root but let use a positve root

We are taking the positve roots

Plug 9 as n into n+1

`9 + 1 = 10`

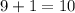
or

`- 10 + 1 = - 9`