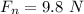Question

A 1-kg book is at rest on a desk. Determine the force the desk exerts on the book
​

Answer 1

`\displaystyle F_n = 9.8 \ N`

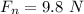
General Formulas and Concepts:

Math

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Physics

Forces

SI Unit: Newtons N

Free Body Diagrams

Gravitational Force:
`\displaystyle F_g = mg`

• m is mass (in kg)
• g is Earth's gravity (9.8 m/s²)

Normal Force:
`\displaystyle F_n`

Newton's Law of Motions

1. Newton's 1st Law of Motion: An object at rest remains at rest and an object in motion stays in motion
2. Newton's 2nd Law of Motion: F = ma (Force is equal to [constant] mass times acceleration)
3. Newton's 3rd Law of Motion: For every action, there is an equal and opposite reaction

Step-by-step explanation:

Step 1: Define

1 kg book at rest

Step 2: FBD

See Attachment

Draw a free body diagram to label the forces acting upon the book. We see that we would have gravitational force from Earth pointing downwards and normal force from the surface of the desk pointing upwards.

Since the book is not moving, we know that ∑F = 0 (sum of forces equal to 0).

Step 4: Find Normal Force

1. Define Forces [Newton's Law of Motions]:
   `\displaystyle \sum F = 0`
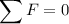
2. [Newton's Law of Motions] Substitute in forces:
   `\displaystyle F_g - F_n = 0`
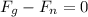
3. [Newton's Law of Motions] [Addition Property of Equality] Isolate
   `\displaystyle F_n`:
   `\displaystyle F_g = F_n`
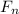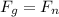
4. [Newton's Law of Motions] Substitute in
   `\displaystyle F_g`:
   `\displaystyle mg = F_n`
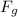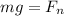
5. [Newton's Law of Motions] Rewrite:
   `\displaystyle F_n = mg`
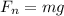
6. [Newton's Law of Motions] Substitute in variables:
   `\displaystyle F_n = (1 \ kg)(9.8 \ (m)/(s^2))`
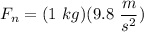
7. [Newton's Law of Motions] Multiply:
   `\displaystyle F_n = 9.8 \ N`