Answer:
True
Explanation:
To answer this question, I will use the following illustrations.
Assume a point (x,y) is reflected across the x-axis.
Using reflection rule, the new point will be: (x,-y)
On a coordinate plane, the x-axis is represented as: (x,0)
So, we will calculate the distance between (x,y) and (x,0) and also calculate the distance between (x,-y) and (x,0) using the following distance formula.
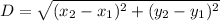
Distance between (x,y) and (x,0)
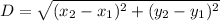
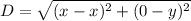
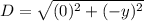

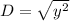
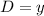
Distance between (x,-y) and (x,0)
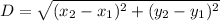
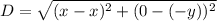
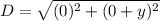

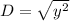
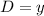
See that the calculated distance are equal.
Hence, the given statement is true