Question

Mercury has the most eccentric (least circular) orbit of all the planets in the Solar System. At aphelion it is 0.467 AU from the Sun while at perihelion it is only 0.308 AU from the Sun. What is Mercury's orbital period in Earth-days?

Answer 1

Mercury's orbital period is approximately 88 days

Step-by-step explanation:

Mercury's orbit parameters given in the question are;

Mercury's aphelion distance, Rₐ = 0.467 AU

Mercury's perihelion distance,
`R_p` = 0.308 AU

Therefore, the average distance from Mercury to the Sun, 'a', is given as follows;

`a = (R_a + R_p)/(2)`

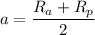
By plugging in the values of 'Rₐ' and '
`R_p`', we get;

`a = (R_a + R_p)/(2) = (0.467 \, AU + 0.308 \, AU)/(2) = 0.3875 \, AU`

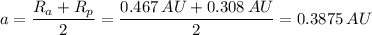
a = 0.3875 AU

According to Kepler's third law, we have;

P² = k·a³

Where;

P = The orbital period of the plane

a = The average distance from Mercury to the Sun

k = Constant

When k = 1, we have;

P² = a³

∴ P = √(a³)

From which we have;

P = √(0.3875 AU)³ ≈ 0.241216804711 years

P ≈ 0.2412168 years

1 year = 365 days

∴ 0.241216804711 years = 0.241216804711 years × 365 days/year ≈ 88.0441337 days

0.241216804711 years ≈ 88.0441337 days ≈ 88 days

Mercury's orbital period, P ≈ 88 days.