In △LMN, Anthony claims it is isosceles. Calculating the length of segment LM using the distance formula yields
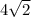 , confirming Anthony's claim and providing a quantitative measure of the triangle's side.
, confirming Anthony's claim and providing a quantitative measure of the triangle's side.
The distance (d) between two points
 and
and
 is calculated using the distance formula:
is calculated using the distance formula:
![\[ d = √((x_2 - x_1)^2 + (y_2 - y_1)^2) \]](https://img.qammunity.org/2024/formulas/mathematics/college/c11pfjm3s03a2uhvm93e73mvj3qxrtscm2.png)
For segment LM
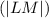 , using coordinates (L (3, 4)) and (M (7, 8)):
, using coordinates (L (3, 4)) and (M (7, 8)):
![\[ |LM| = √((7 - 3)^2 + (8 - 4)^2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/qzlngth8dgouvpupajcjah59ch586r93q7.png)
![\[ |LM| = √(4^2 + 4^2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/nn9e5h5748q6zjzzcq011qwizfxfnitycd.png)
![\[ |LM| = √(32) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/hcghn3m8m3lmoj754sq54vn599l4nffs0p.png)
Thus, the length of segment LM is
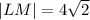 .
.
The question probable may be:
Anthony asserts that △LMN is an isosceles triangle. Given the coordinates of points (L (3, 4)), (M (7, 8)), and (N (5, 12)), calculate the length of segment LM using the distance formula.