Answer:
4.
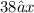
3.
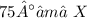
2.
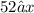
1.
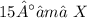
Explanation:
Before we begin, here are the formulas for both laws:
Solving for Angles
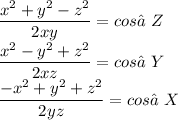
Do not forget to use
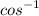 in the end or you will throw the result off!
in the end or you will throw the result off!
Solving for Edges
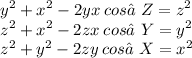
Take the square root of the end result or you will throw it off!
-----------------------------------------------------------------------------------
Solving for Angles
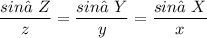
Do not forget to use
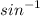 in the end or you will throw the result off!
in the end or you will throw the result off!
Solving for Edges
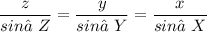
_____________________________________________
4.
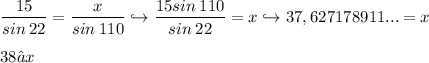
3.
![\displaystyle (-19^2 + 17^2 + 14^2)/(2[17][14]) = cos∠X \hookrightarrow (-361 + 289 + 196)/(476) = cos∠X \hookrightarrow 0,2605042016... = cos∠X; 74,900018217...° = cos^(-1)\:0,2605042016... \\ \\ 75° ≈ m∠X](https://img.qammunity.org/2022/formulas/mathematics/high-school/9nfhy37b7kx0h56i80clh3z7adlb7atgqk.png)
2.
![\displaystyle 16^2 + 42^2 - 2[42][16]\:cos\:120 = x^2 \hookrightarrow 256 + 1764 - 1344\:cos\:120 = x^2 \hookrightarrow √(2692) = √(x^2); 2√(673)\:[or\:51,884487084...] = x \\ \\ 52 ≈ x](https://img.qammunity.org/2022/formulas/mathematics/high-school/9fxj9x67ygx84bboxzcm8kf1msbsd9tqd1.png)
You could have also used the Law of Sines sinse the base angles are congruent [30°].
1.
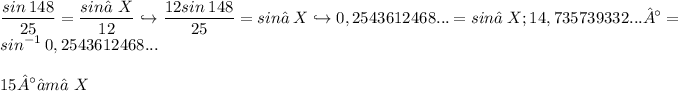
I am joyous to assist you at any time.