Question

Select the correct answer.

Solve the system of equations.

y = x + 3

`y=x^(2) +7x+8`

A.
(-1,-4) and (-5,-8)
B.
(-1,2) and (-5,-2)
C.
(1,4) and (5,8)
D.
(-1,-2) and (-5,2)

Answer 1

B. (-1,2) and (-5,-2)

Explanation:

Substitute x + 3 in for y in the second equation. you get

`x + 3 = x^(2) + 7x + 8\\x^(2) + 6x + 5 = 0`

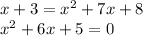
(x + 1)(x + 5) = 0

x + 1 = 0 or x + 5 = 0

x = - 1 or x = -5

Using the first equation, let x = -1 and x = -5 in order to get the corresponding values for y

y = -1 + 3 = 2 and y = -5 + 3 = -2

So, B is the correct answer.