Question

AP Calc BC help!

Can someone explain how to do these problems? I care more about the explanation than the actual answer! My course never taught me how to do these kinds of problems.
Thank you!!

Answer 1

Question 1) 72

Question 2) 40

Question 3) Both C and D.

Question 4) Both A and C.

Explanation:

Question 1)

We are given that:

`\displaystyle \int_1^5f(x)\, dx=8\text{ and we want to find} \int_1^5xf'(x)\, dx`

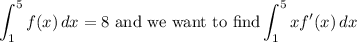
We will use integration by parts, given by:

`\displaystyle \int_a^b u\, dv=uv-\int_a^b v\, du`

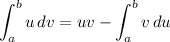
We will let:

`u=x\Rightarrow du=dx\text{ and } dv=f'(x)\, dx \Rightarrow v=f(x)`

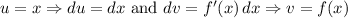
Therefore:

`\displaystyle \int_1^5xf'(x)\, dx=xf(x)\Big|_1^5-\int_1^5f(x)\, dx`

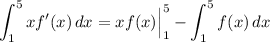
Substitute:

`\displaystyle \int_1^5xf'(x)\, dx=(5(f(5))-(1(f(1))-(8)`

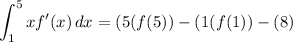
Evaluate:

`\displaystyle \int_1^5xf'(x)\, dx=75-(-5)-8=72`

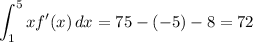
Question 2)

Similarly, we will let:

`\displaystyle u=x\Rightarrow du=dx\text{ and } dv=f'(x)\, dx \text{ so } v=f(x)`

Hence:

`\displaystyle \int_0^3 xf'(x)\, dx=xf(x)\Big|_0^3-\int_0^3f(x)\, dx`

Evaluate:

`\displaystyle \int_0^3 xf'(x)\, dx=(3f(3))-(0(f(0))-(2)`

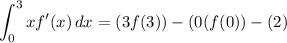
Thus:

`\displaystyle \int_0^3 xf'(x)\, dx=3(14)-2=40`

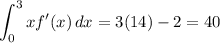
Question 3)

We are given:

`\displaystyle g(x)=\int_4^xf(x)\, dx`

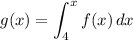
By the Fundamental Theorem of Calculus:

`g'(x)=f(x)>0`

The derivative of g is always positive. So, the values of g are always increasing.

The tables that reflect this are C and D.

And there are, as I understand it, no way to determine their exact values. Both C and D are correct.

Question 4)

Similarly, we are given:

`\displaystyle g(x)=\int_(-2)^xf(x)\, dx`

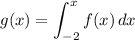
By the FTC:

`g'(x)=f(x)<0`

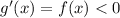
So, g should be decreasing for all x.

The tables that reflect this are A and C.

So, both A and C are correct.