Question

Someone help me Please!!!

Answer 1

Answer: (-2, -1) and (3, 14).

Explanation:

`\left \Bigg \{ { \bigg{y=x^(2) +2x-1} \atop \bigg {y-3x=5}} \right. ; \left \Bigg \{ { \bigg{y=x^(2) +2x-1} \atop \bigg {y=5+3x}} \right.`

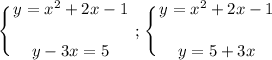
x² + 2x - 1 = 5 + 3x

x² + 2x - 1 - 5 - 3x = 0

x² - x - 6 = 0

`General formula\\\\x=\frac{-b \pm \sqrt{b^(2)-4ac } }{2a} \\\\a=1; \: \: b=-1; \: \: c=-6\\\\x=\frac{1 \pm \sqrt{(-1)^(2)-4 \cdot1 \cdot (-6)} }{2 \cdot 1}=\frac{1 \pm√(25) } {2} =(1 \pm5)/(2) \\\\x_(1) = -2\\x_(2) =3`

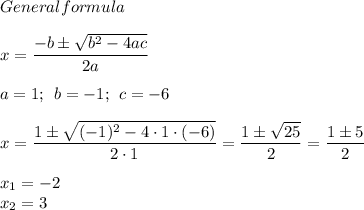
y = 5 + 3x

y₁ = 5 + 3 * (-2) = -1

y₂ = 5 + 3 * 3 = 14

The pair of points representing the solution set of this system of equations is (-2, -1) and (3, 14).