79
============
The general formula for the nth term of an arithmetic sequence is given by:
where:
 is the first term,
is the first term,
 is the term number,
is the term number,
 is the common difference.
is the common difference.
In this case, you are given:
-
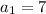 (the first term is 7),
(the first term is 7), -
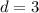 (the common difference is 3),
(the common difference is 3), -
 (we're looking for the 25th term).
(we're looking for the 25th term).
We'll plug these values into the general formula to find the 25th term:
So, the 25th term of the arithmetic sequence is 79.