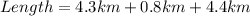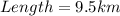Question

A running race follows a triangular course. The first leg of the race is in a straight line, covering 4.4km. Runners turn an angle of 79 deg for the second leg, and then turn again 77 deg to head back to the start line to finish the race. What is the length of the entire race, to the nearest tenth of a kilometer?

Answer 1

The length of the entire race is 9,5km

Explanation:

Required

Determine the length of the race.

To aid my explanation, I have added an attachment which shows the triangular course.

From the attachment, we have:

A as the starting point and the following measurement;

`\angle B = 11^{\circ`

`\angle C = 13^(\circ) + 79^(\circ) = 92^{\circ`

`\angle A + \angle B + \angle C = 180^(\circ)`

`\angle A = 180^(\circ) - (\angle B + \angle C )`

`\angle A = 180^(\circ) - (11^(\circ)+92^(\circ))`

`\angle A = 77^(\circ)`

`\angle B = 11^{\circ`

`\angle C = 92^{\circ`

`c = 4.4km`

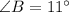
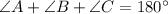
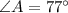
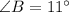
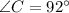
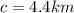
Apply sine rule

`(a)/(sin\ A) = (b)/(sin\ B) = (c)/(sin\ C)`

`(a)/(sin\ 77^(\circ)) = (b)/(sin\ 11^(\circ)) = (4.4)/(sin\ 92^(\circ))`

`(a)/(sin\ 77^(\circ)) = (b)/(sin\ 11^(\circ)) = (4.4)/(0.9994)`

`(a)/(sin\ 77^(\circ)) = (b)/(sin\ 11^(\circ)) = 4.403`

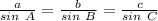
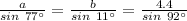
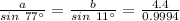
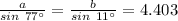
Split to solve for a and b

`(a)/(sin\ 77^(\circ)) =4.403`

`(b)/(sin\ 11^(\circ)) = 4.403`

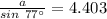
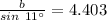
Make a the subject

`(a)/(sin\ 77^(\circ)) =4.403`

`a = 4.403 * sin(77^(\circ))`

`a = 4.403 * 0.9744`

`a = 4.3km`

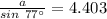
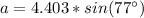
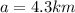
Make b the subject

`(b)/(sin\ 11^(\circ)) = 4.403`

`b = 4.403 * sin(11^(\circ))`

`b = 4.403 * 0.1908`

`b = 0.8km`

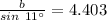
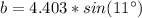
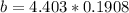
The length of the race is:

`Length = a + b + c`

`Length = 4.3km + 0.8km + 4.4km`

`Length = 9.5km`