Question

This square root equation has 2 solutions. what is the extraneous solution​

Answer 1

-7

Explanation:

Solving an equation and finding the extraneous solution.

Extraneous solution are the values that we obtain when solving the equations that aren't true solutions to the equation.

`\sf √(x + 11) - 5 = x\\\text{\bf Add 5 to both sides,}\\\\√(x + 11) = x + 5\\\\\text{\bf Now, square both sides}\\\\(√(x+11))^2= (x + 5)^2\\\\x + 11 = x^2 + 2*x*5 + 5^2 \ ~~~~~ \text{Use the identity:} \ (a + b)^2 = a^2 + b^2 + 2ab\\\\x + 11 = x^2 + 10x + 25\\\\0 = x^2 + 10x + 25 - x - 11`

x² + 10x -x + 25 - 11 = 0

x² + 9x + 14 = 0

Product = 14

Sum = 9

Factors = 7, 2 { 7*2 = 14 & 7 +2 = 9}

Rewrite the middle term using the factors.

x² + 2x + 7x + 14 = 0

x(x + 2 ) + 7(x + 2) =0

(x +2)(x + 7) = 0

x + 2 = 0 ; x + 7 = 0

x = -2 ; x = -7

Now, substitute x = -2 in the given equation,

`\sf √(-2+11) -5 = -2\\\\~~~~~~~~ ~~√(9) -5 = -2\\\\`

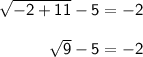
3 - 5 = -2

-2 = -2

So, x = -2 is a true solution.

Substitute x = -7 in the given equation,

`\sf √(-7+11)-5 = -7\\\\~~~~~~~~~ √(4)-5 = -7\\\\~~~~~~~~~~~ 2 - 5 = -7\\\\`.

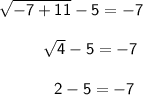-3 ≠ -7

So, x = -7 is an extraneous solution